...making Linux just a little more fun!
By Ariel Ortiz Ramirez
|
...making Linux just a little more fun! |
By Ariel Ortiz Ramirez |
C# (pronounced C-sharp) is a new object-oriented programming language designed to take advantage of Microsoft's .NET development framework. It has many similarities with other popular object-oriented languages such as C++ and Java, yet it offers some new goodies.
Linux offers the opportunity to develop C# applications thanks to a project called Mono. Mono is an open source implementation of the .NET platform. In the following sections, I will describe the main elements of the current implementation of the Mono system.
At this time, Mono implements two standards: the C# programming language (Standard ECMA-334) and the Common Language Infrastructure (Standard ECMA-335). Both of these specifications were developed by Microsoft and submitted to ECMA (a vendor consortium formerly known as the European Computer Manufacturers Association) on October 2000. They were formally approved on December 2001, and they will probably become ISO standards (thanks to a "fast-track" agreement that ISO has with ECMA) some time before the end of next year.
The Mono project is sponsored by Ximian, the same company that brought us the GNOME graphical desktop environment. Mexican hacker and Ximian CTO Miguel de Icaza currently leads the development of this project. In my opinion, the people involved with the development of Mono have done a remarkable job in quite a short amount of time. By the way, the word "Mono" means monkey in Spanish. These guys at Ximian really like monkeys.
Lets follow a simple programming example in order to understand how C# and the different Mono components fit together. To see this in action, make sure you have a working Mono installation (see the resources section for information on downloading and installing Mono).
The following figure summarizes the process we will follow in order to compile and run our C# program:
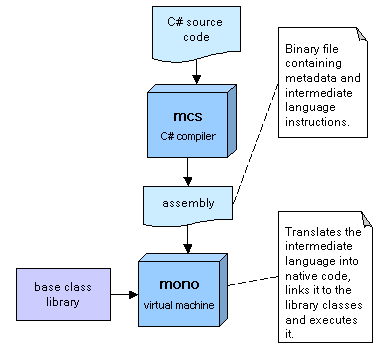
First, we will create a simple C# source program (the classical "Hello World!" couldn't be missing). Type the following program using your favorite text editor and save the file as hello.cs:
class Hello {
public static void Main() {
System.Console.WriteLine("Hello Mono World!");
}
}
This program is composed of a class named Hello which contains
a method called Main. This method establishes the program entry
point, in the same way that the main function is the start of a
C/C++ program. In this example, the Main method prints to the
standard output the message "Hello Mono World".
We can now
compile the program using the Mono C# compiler, called mcs. At the
shell prompt type:
mcs hello.cs
We now should have a file called hello.exe in the current directory. But don't get baffled about the .exe file name extension. It is not a Windows executable file, at least not in the way we're used to. Contrary to what happens when we compile a program written in languages like C or C++, the C# compiler does not generate a machine-specific object file (for example a Linux ELF x86 object file), but instead generates a special binary file called an assembly, which is made up of metadata and intermediate language (IL) instructions. These two together represent a platform-agnostic translation of the program source code. This means, of course, that when we actually run the program contained in the assembly, its intermediate language code has to be translated to the native code of the computer where the program is being run. This last translation phase is carried out by a virtual machine, whose behavior is defined by the Common Language Infrastructure (CLI) specification. The CLI defines an object oriented runtime environment that supports a base class library, dynamic class loading and linking, multiple thread execution, just-in-time compilation, and automatic memory management. The Microsoft implementation of the CLI specification is usually referred as the Common Language Runtime (CLR). We say that the CLR is a superset of the CLI because the CLR contains some extensions that are not part of the CLI.
To execute our assembly, we must invoke the program called mono,
which is the Mono virtual machine. Type at the shell prompt the following:
mono hello.exe
The output should be:
Hello Mono World!
Lets see how to examine the contents of our assembly. The program monodis
(Mono disassembler) reads the binary information of an assembly and
produces a textual representation of its contents. Type at the shell prompt:
monodis hello.exe
The disassembler output should be something like the following:
.assembly extern mscorlib
{
.ver 0:0:0:0
}
.assembly 'hello'
{
.hash algorithm 0x00008004
.ver 0:0:0:0
}
.class private auto ansi beforefieldinit Hello
extends [mscorlib]System.Object
{
// method line 1
.method public hidebysig specialname rtspecialname
instance default void .ctor() cil managed
{
// Method begins at RVA 0x20ec
// Code size 7 (0x7)
.maxstack 8
IL_0000: ldarg.0
IL_0001: call instance void valuetype [corlib]System.Object::.ctor()
IL_0006: ret
} // end of method instance default void .ctor()
// method line 2
.method public static
default void Main() cil managed
{
// Method begins at RVA 0x20f4
.entrypoint
// Code size 11 (0xb)
.maxstack 8
IL_0000: ldstr "Hello Mono World!"
IL_0005: call void class [corlib]System.Console::WriteLine(string)
IL_000a: ret
} // end of method default void Main()
} // end of type Hello
The first part of this output corresponds to the metadata. It contains
information about the current version of the assembly, any optional security constraints,
locale information, and a list of all externally referenced assemblies that are
required for proper execution. The rest of the output represents the IL code. We
can spot two methods in this code: the default class constructor called .ctor,
provided automatically by the compiler, and our Main method. As
described before, when the virtual machine is asked to run this code, it uses a
just-in-time (JIT) compiler to translate the IL into the native machine code of the
hosting environment. The native code is not generated until it is actually
needed (thus the name just-in-time). For our example, the following is the native x86
machine code (in AT&T assembly language syntax) that gets generated for the Main
method:
push %ebp mov %esp,%ebp sub $0x30,%esp push $0x80c9eb0 mov 0x805462c,%eax push %eax cmpl $0x0,(%eax) mov (%eax),%eax call *0x94(%eax) add $0x8,%esp mov 0x805462c,%eax push %eax cmpl $0x0,(%eax) mov (%eax),%eax call *0xb4(%eax) add $0x4,%esp leave ret
Mono also comes with an interpreter called mint. If you use this
program, the IL instructions are interpreted instead of being compiled to native
code by the JIT. Actually, our simple program might be a little bit faster when
run under mint because the JIT compiler will take some time to
compile the code of our program and store it some where in memory. Of course,
subsequent execution of the native code already in memory is definitely faster
than interpretation. Currently the Mono JIT compiler is only available for x86
machines. The Mono interpreter must be used in any non-x86 machine. To see the
interpreter running, type at the shell prompt:
mint hello.exe
If you're familiar with Java, you might be thinking that all this technology sounds pretty much like the way that the Java platform works. And this is indeed so. The CLI virtual machine is the key factor for platform independence. This means that I can write and compile a program in Linux using Mono, and then run it in a Windows computer with the .NET framework. There is no need to rewrite or recompile the source code. But in contrast to the Java Virtual Machine, which is tightly coupled to the Java programming language, the CLI specification not only allows platform independence, it also allows language independence. Windows has compilers that target the CLR from a number of languages. The most important ones are part of Microsoft's Visual Studio .NET development environment: Visual Basic .NET, JScript .NET, Managed C++ and C#. Other languages supported, from third party vendors, include APL, COBOL, Eiffel, Forth, Fortran, Haskell, Mercury, Mondrian, Oberon, Pascal, Perl, Python, RPG, Scheme and SmallScript. The Mono project only has a C# compiler at this time, but we will probably see in the near future other languages being supported.
Another important element of the CLI is the Common Type System (CTS). The CTS fully describes all the data types supported by the virtual machine, including how these data types interact with each other and how they are represented as metadata inside the assemblies. It is important to note that not all languages available for the CLI support all data types in the CTS. So there is a Common Language Specification (CLS), that defines a subset of common types that ensure that binary assemblies can be used across all languages that target the CLI. This means that if we build a CLI class that only exposes CLS compliant features, any CLI compatible language can use it. You could create a class in Eiffel, subclass it in C# and instantiate it in a Visual Basic.NET program. Now this is real language interoperability.
Using a CLI compliant platform, such as Mono or the .NET framework, has some important advantages:
C#, as a programming language, has also some important features:
I will discuss these and other C# issues more thoroughly in later articles.