Python for scientific use, Part II: Data analysis
Introduction
In Linux Gazette issue #114, we took the first steps towards understanding and interpretation of scientific data by using Python for the visualization. The next step is to reach a quantitative understanding by performing some sensible data analysis, such as fitting a model to the data and thereby extracting useful parameters. This defines the main topic of this part II of Python for scientific use. As with part I, this article will also be centered around a few illustrative examples. I assume that the reader is familiar with either part I of this article or basic Python.
Part I: post scriptum
As a pleasant surprise, I actually got some nice reader feedback related to Part I of this article. Some readers proposed additional tips & tricks; I have included them here, to the service of other readers who might find it useful (at least I did :-).
If you want to try out all the examples on a Wind0ws machine (for some
wicked reason), John Bollinger suggested to use os.popen the
following way:
f=os.popen('pgnuplot.exe','w')
Even more intelligently, the following code ensures that the Python script can be run on both Linux and Wind0ws:
import os
import sys
if os.name == 'posix':
f=os.popen('gnuplot', 'w')
print 'posix'
elif os.name == 'nt':
f=os.popen('pgnuplot.exe', 'w')
print 'windows'
else:
print 'unknown os'
sys.exit(1)
JB also pointed my attention to Michael Haggerty's neat
project, gnuplot.py,
at sourceforge.
Cyril Buttay brought to my attention that the default encoding in gnuplot is insufficient if you want to print special characters, e.g. Danish ones like æ, ø, and å on the plots. In order to do so, you need to specify another encoding as described in the gnuplot manual:
set encoding {<value>}
show encoding
where the valid values are
default - tells a terminal to use its default encoding
iso_8859_1 - the most common Western European font used by many
Unix workstations and by MS-Windows. This encoding is
known in the PostScript world as 'ISO-Latin1'.
iso_8859_2 - used in Central and Eastern Europe
iso_8859_15 - a variant of iso_8859_1 that includes the Euro symbol
cp850 - codepage for OS/2
cp852 - codepage for OS/2
cp437 - codepage for MS-DOS
koi8r - popular Unix Cyrillic encoding
If the encoding is not changed from the default, the special character might
show up on the screen but not in the hardcopy (actually, I think the
special characters only work with terminal postscript, but I'm
not sure). If the desired special character is not available on your
keyboard, it can be accessed though its octal value; e.g., to print a special
character such as the Danish å in the title of a plot, set the encoding to
iso_8859_1:
set title "This is a Danish character \345"
which will display This is a Danish character å in
the title of the plot. To also use Greek characters, e.g. α (lowercase
alpha), one should use {/Symbol a} (this requires
terminal postscript enhanced). Similar, Γ (uppercase
gamma), is generated with {/Symbol G}. To find special
characters and their corresponding octal values for, e.g.,
iso8859-1 encoding in Linux, just type:
man iso_8859-1
or have a look at this postscript file.
[ If you're not sure of the exact name of the relevant manpage, just type
man -k string, where 'string' is the name, or part of
the name of the encoding you're looking for. This will get you a list of
all the manpages the names of which contain that string. -- Ben ]
Example 1: Fitting 2-D data
The first example illustrates how to fit a model to 2-D data. The data to be fitted is included in the file tgdata.dat and represents weight loss (in wt. %) as a function of time. The weight loss is due to hydrogen desorption from LiAlH4, a potential material for on-board hydrogen storage in future fuel cell powered vehicles (thank you Ben for mentioning hydrogen power in the Laundrette in issue #114). The data is actually the same as in example 1 of LG#114. For some reason, I suspect that the data may be explained by the following function:
f(t) = A1*(1-exp(-(k1*t)^n1)) + A2*(1-exp(-(k2*t)^n2))
There are different mathematical methods available for finding the parameters that give an optimal fit to real data, but the most widely used is probably the Levenberg-Marquandt algorithm for non-linear least-squares optimization. The algorithm works by minimizing the sum of squares (squared residuals) defined for each data point as
(y-f(t))^2
where y is the measured dependent variable and
f(t) is the calculated. The Scipy package has the Levenberg-Marquandt
algorithm included as the function leastsq.
The fitting routine is in the file kinfit.py and the python code is listed below. Line numbers have been added for readability.
1 from scipy import *
2 from scipy.optimize import leastsq
3 import scipy.io.array_import
4 from scipy import gplt
5
6 def residuals(p, y, x):
7 err = y-peval(x,p)
8 return err
9
10 def peval(x, p):
11 return p[0]*(1-exp(-(p[2]*x)**p[4])) + p[1]*(1-exp(-(p[3]*(x))**p[5] ))
12
13 filename=('tgdata.dat')
14 data = scipy.io.array_import.read_array(filename)
15
16 y = data[:,1]
17 x = data[:,0]
18
19 A1_0=4
20 A2_0=3
21 k1_0=0.5
22 k2_0=0.04
23 n1_0=2
24 n2_0=1
25 pname = (['A1','A2','k1','k2','n1','n2'])
26 p0 = array([A1_0 , A2_0, k1_0, k2_0,n1_0,n2_0])
27 plsq = leastsq(residuals, p0, args=(y, x), maxfev=2000)
28 gplt.plot(x,y,'title "Meas" with points',x,peval(x,plsq[0]),'title "Fit" with lines lt -1')
29 gplt.yaxis((0, 7))
30 gplt.legend('right bottom Left')
31 gplt.xtitle('Time [h]')
32 gplt.ytitle('Hydrogen release [wt. %]')
33 gplt.grid("off")
34 gplt.output('kinfit.png','png medium transparent size 600,400')
35
36 print "Final parameters"
37 for i in range(len(pname)):
38 print "%s = %.4f " % (pname[i], p0[i])
In order to run the code download the kinfit.py.txt file as kinfit.py (or
use another name of your preference), also download the datafile tgdata.dat and run the script with
python kinfit.py. Besides Python, you need to have SciPy and
gnuplot installed (vers. 4.0 was used throughout this article). The output
of the program is plotted to the screen as shown below. A hard copy is also
made. The gnuplot png option size is a little tricky. The
example shown above works with gnuplot compiled against libgd.
If you have libpng + zlib installed, instead of
size write picsize and the specified width and
height should not be comma separated. As shown in the figure below, the
proposed model fit the data very well (sometimes you get lucky :-).
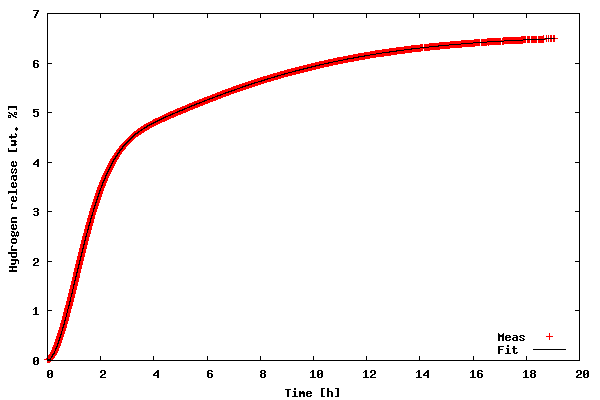
Now, let us go through the code of the example.
- Line 1-4
- all the needed packages are imported. The first is basic SciPy functionality, the second is the Levenberg-Marquandt algorithm, the third is ASCII data file import, and finally the fourth is the gnuplot interface.
- Line 6-11
- First, the function used to calculate the residuals (not the squared
ones, squaring will be handled by
leastsq) is defined; second, the fitting function is defined. - Line 13-17
- The data file name is stored, and the data file is read using
scipy.io.array_import.read_array. For convenience x (time) and y (weight loss) values are stores in separate variables. - Line 19-26
- All parameters are given some initial guesses. An array with the names of the parameters is created for printing the results and all initial guesses are also stored in an array. I have chosen initial guesses that are quite close to the optimal parameters. However, chosing reasonable starting parameters is not always easy. In the worst case, poor initial parameters might result in the fitting procedure not being able to find a converged solution. In this case, a starting point can be to try and plot the data along with the model predictions and then "tune" the initial parameters to give just a crude description (but better than the initial parameters that did not lead to convergence), so that the model just captures the essential features of the data before starting the fitting procedure.
- Line 27
- Here the Levenberg-Marquandt algorithm (
lestsq) is called. The input parameters are the name of the function defining the residuals, the array of initial guesses, the x- and y-values of the data, and the maximum number of function evaluation are also specified. The values of the optimized parameters are stored inplsq[0](actually the initial guesses inp0are also overwritten with the optimized ones). In order to learn more about the usage oflestsqtypeinfo(optimize.leastsq)in an interactive python session - remember that the SciPy package should be imported first - or read the tutorial (see references in the end of this article). - Line 28-34
- This is the plotting of the data and the model calculations (by evaluating the function defining the fitting model with the final parameters as input).
- Line 36-38
- The final parameters are printed to the console as:
Final parametersA1 = 4.1141A2 = 2.4435k1 = 0.6240k2 = 0.1227n1 = 1.7987n2 = 1.5120
Gnuplot also uses the
Levenberg-Marquandt algorithm for its built-in curve fitting procedure.
Actually, for many cases where the fitting function is somewhat simple and
the data does not need heavy pre-processing, I prefer gnuplot over Python -
simply due to the fact that Gnuplot also prints standard error estimates of
the individual parameters. The advantage of Python over Gnuplot is the
availability of many different optimization algorithms in addition to the
Levenberg-Marquandt procedure, e.g. the Simplex algorithm, the Powell's
method, the Quasi-Newton method, Conjugated-gradient method, etc. One only
has to supply a function calculating the sum of squares (with
lestsq squaring and summing of the residuals were performed
on-the-fly).
Example 2: Sunspots
In the next example we will use the Fast Fourier Transform (FFT) in order to transform time-dependent data into the frequency domain. By doing so, it is possible to analyse if any predominant frequencies exists - i.e. if there is any periodicity in the data. We will not go into too much detail of the underlying mathematics of the FFT method; if you're interested, have a look at some of the many informative pages on the internet, e.g. http://astronomy.swin.edu.au/~pbourke/analysis/dft/, http://www.cmlab.csie.ntu.edu.tw/cml/dsp/training/coding/transform/fft.html, Numerical recipes, etc.
Let's take a simple example to get started. Consider temperature measurement at a given location as a function of time. By intuition, we expect such data to have a dominant frequency component of 1/24h = 0.042 h-1 simply reflecting the fact that it is usually warmer during the day (with a maximum around noon) and cooler during the night (with a minimum sometime during the night). Thus, assuming a period with stable weather for, say, one week, we may approximate the the temperature variations as a function of time with a sine wave with a period of 24 h. If we take the Fourier Transform of this sine wave we find that only one single frequency is present (shown as a δ-function) and that it is 0.042 h-1. OK, enough with the simple case, if everything was this simple we wouldn't need the Fourier Transform. Instead we will move to a more complex case where intuition is not enough.
The example data we will use is the sunspot activity measurements from year 1700 to year 2004 provided by National Geophysical Data Center - NOAA Sattelite and Information Service. The data set is the yearly sunspot observations available via FTP. The datafile is also included as sunspots.dat. The sunspot data have been used for illustrating the power of FFT with respect to finding a periodicity in sunspot activity in various computer languages, e.g. Matlab and BASIC. The observations that there is (or might be) a correlation between sunspot activity and the global temperature have led to controversy when discussing the greenhouse effect and global warming.
The graph below illustrates the sunspot data to be used in this example.
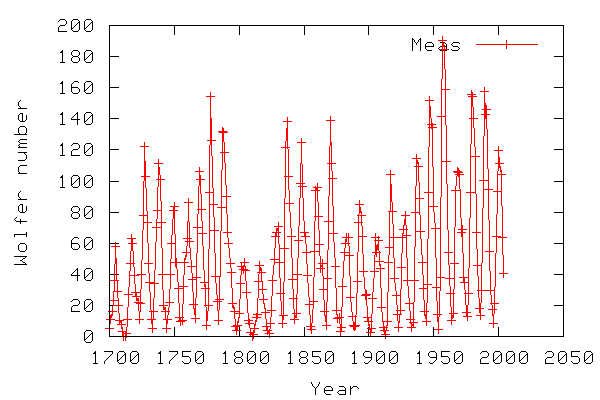
The code below shows the python script for analysing the sunspot data. The shown script is a shortened version with some plots removed. The full script is in sunspots.py.txt.
1 from scipy import *
2 import scipy.io.array_import
3 from scipy import gplt
4 from scipy import fftpack
5
6 sunspot = scipy.io.array_import.read_array('sunspots.dat')
7
8 year=sunspot[:,0]
9 wolfer=sunspot[:,1]
10 Y=fft(wolfer)
11 n=len(Y)
12 power = abs(Y[1:(n/2)])**2
13 nyquist=1./2
14 freq=array(range(n/2))/(n/2.0)*nyquist
15 period=1./freq
16 gplt.plot(period[1:len(period)], power,'title "Meas" with linespoints')
17 gplt.xaxis((0,40))
18 gplt.xtitle('Period [year]')
19 gplt.ytitle('|FFT|**2')
20 gplt.grid("off")
21 gplt.output('sunspot_period.png','png medium transparent picsize 600 400')
In the first few lines we import all the necessary packages. In line 6 the
sunspot data is imported and stored in the variable sunspot;
for convenience the x-values (year) and y-values (Wolfer number) are stored
in separate variables. In line 10 we take the fast Fourier transform (FFT)
of the sunspot data. As shown in the figure below, the output is a
collection of complex numbers (defining both amplitude and phase of the
wave components), and there is noticeable symmetry around Im=0.
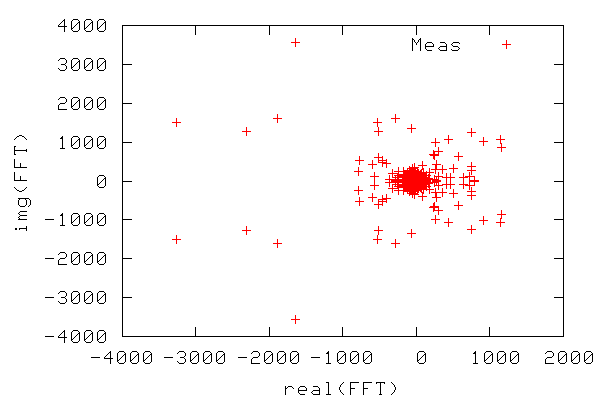
In order to construct a periodogram, i.e. a graph of power vs. frequency, we first compute the power of the FFT signal which is simply the FFT signal squared. We only need the part of the signal ranging from zero to a frequency equal to the Nyquist frequency, which is equal to half the maximum frequency, since frequencies above the Nyquist frequency correspond to negative frequencies. The frequency range is calculated from 0-N/2 as N/(2T) where N is the number of samples and T is the sampling time. The figure below shows the resulting periodogram.
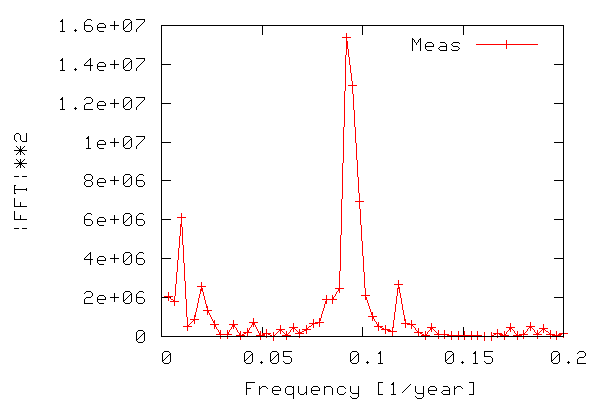
Thus, we can see that there is indeed periodicity in the sunspot data, with frequencies around 0.9 standing out. Note that it is easier to see if we use the period (inverse of frequency) instead of frequency on the x-axis.
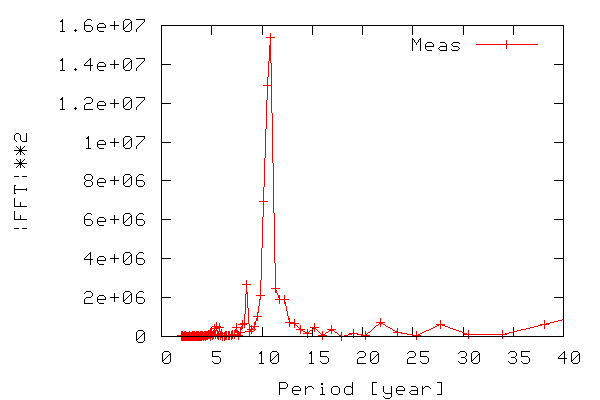
As seen in the figure we have found out (like many others have) that the sunspot activity data from 1700-2004 is periodic, and that the sunspots occur with a maximum in activity approx. every 11 years.
Example 3: Fitting multiple 2-D data files
The next and final example is a little more complex than the previous ones.
The task it should accomplish is to cycle through a number of data files
(similar to the ones used in Example 3 of Part I) and take a slice of each data
file, corresponding to an X-ray diffraction
peak as shown in example 2 in Part I.
To this peak a Gaussian (bell)
curve should be fitted and the fitting parameters should be stored in a
datafile. The extracted parameters: peak position, peak height, peak width,
all contain valuable information about the sample under investigation
(MgH2, another material for solid state hydrogen storage). The
peak position is related to the crystal lattice of the material (actually
the interatomic spacing, if we're to be precise), the peak height
corresponds to the abundance of the material, and the peak width
corresponds to the domain size of the MgH2 crystallites.
Furthermore, the script should take two command line arguments,
plot and data, enabling plotting of the peak fit
as the script cycles through the data files as well as printing out the
fitting parameters to the screen. This option is mainly of diagnostic
nature. Furthermore, there should be some sort of mechanism evaluating the
quality of the fit and in case the fit is poor it should be disregarded.
Finally, the scripts should generate a plot of the fitting parameters as a
function of time (cycle #). The length of the script approaches 100 lines
and will not be shown, but it is stored in the file lgtixrpd.py.txt. In the
following section, I will go though the main parts of the script. To run
the example yourself you'll have to download
and unpack the data files.
- Line 1-3
- The usual import of modules and packages
- Line 5-10
- Setting file names for data files including a data file containing information about temperature vs. cycle number. Setting file names for storing the fitting parameters and the hard copy of the plot.
- Line 12-19
- Setting initial parameters for the fitting routine including
lower and upper bounds for the peak position, peak amplitude/height
(
A), peak position (B), peak half width (C), and the background (D). - Line 21-24
- Read in the temperature data, making a list of data files to be cycled through, and creating data arrays for storing the output.
- Line 26-61
- The main procedure. For each filename in the file list, gnuplot
is used to fit the data (since I prefer to have std. dev. included
in the output as well). If the script is passed a command line
argument called
plotas the first argument, each fit is plotted along the way though the files. In lines 42-53, the state of the fit is evaluated. If, e.g., the amplitude is negative or the peak position is out of bounds, the fit is disregarded and the corresponding fitting parameters are not stored (only zeros are stored). If the script is passed a command line argument calleddata, the fitting parameters are printed to screen as the data files are cycled through. - Line 63-68
- All lines in the data array containing only zeros are removed.
- Line 70-80
- The fitting parameters are stored in ASCII-format in a data file.
- Line 82
- A hard copy of a plot showing temperature, peak amplitude, position and width as a function of time is prepared.
- Line 95-98
- The plot is shown using
ggvand apnmversion of the hard copy is created.
The figure below shows the created plot. From the plot, we notice that during heating (linear) of our sample, the peak position shifts towards lower values. According to Bragg's law of diffraction, there is an inverse relationship between the peak position and the lattice spacing. Thus, our sample expands during heating (as expected). We also observe that when the sample has been heated to 400°C for some time, the amplitude starts decreasing, signaling a disappearance of MgH2 due to decomposition accompanied by the release of hydrogen.
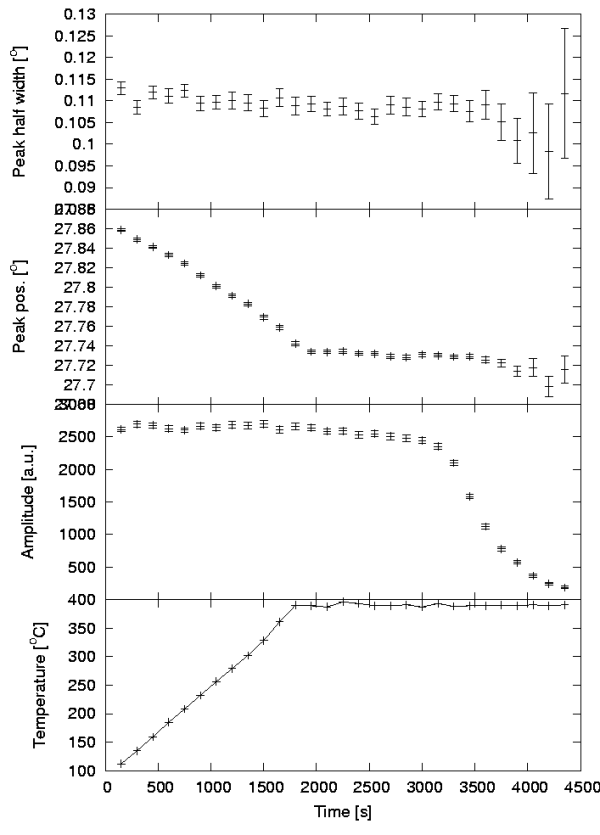
Summary
In this article, a few examples have been given in order to illustrate that Python is indeed a powerful tool for visualization and analysis of scientific data. It combines the plotting power of gnuplot with the power of a real programming language. The SciPy package includes many scientific tools suitable for data analysis.
Suggestions for further reading
Manuals, Tutorials, Books etc:
- Guido van Rossum, Python tutorial, http://docs.python.org/tut/tut.html
- Guido van Rossum, Python library reference, http://docs.python.org/lib/lib.html
- Mark Pilgrim, Dive into Python, http://diveintopython.org/toc/index.html
- Thomas Williams & Colin Kelley, Gnuplot - An Interactive Plotting Program, http://www.gnuplot.info/docs/gnuplot.html
- Travis E. Oliphant, SciPy tutorial, http://www.scipy.org/documentation/tutorial.pdf
- David Ascher, Paul F. Dubois, Konrad Hinsen, Jim Hugunin and Travis Oliphant, Numerical Python, http://numeric.scipy.org/numpydoc/numdoc.htm
See also previous articles about Python published in LG.
Anders has been using Linux for about 6 years. He started out with RH
6.2, moved on to RH 7.0, 7.1, 8.0, Knoppix, has been experimenting a little
with Mandrake, Slackware, and FreeBSD, and is now running Gentoo on his
workstation (no dual boot :-) at work and Debian Sarge on his laptop at
home. Anders has (a little) programming experience in C, Pascal, Bash,
HTML, LaTeX, Python, and Matlab/Octave.
Anders has a Masters degree in Chemical Engineering and is currently
employed as a Ph.D. student at the Materials Research Department, Risö
National Laborary in Denmark. Anders is also the webmaster of Hydrogen storage at Risö.
![[BIO]](../gx/authors/andreasen.jpg)

